Stelling Van Pythagoras
It is called Pythagoras Theorem and can be written in one short equation. Deze euclidische meetkunde gaat over het platte vlak en de ruimte en bevat de alombekende stelling van Pythagoras.

Wiskunde Pythagoras Stelling Gratis Foto Op Pixabay
De stelling is r De stelling is r Ruimtemeetkunde Je komt het de hele dag tegen waarschijnlijk onbewust.

. Although the theorem has long been associated with Greek mathematician-philosopher Pythagoras c. In 2020 verscheen de vernieuwde versie van het ERK. Bij een rechthoekige driehoek geldt de stelling van Pythagoras.
C is the longest side of the triangle. Online studiehulp voor het secundair onderwijs met lesvideos oefeningen toetsen. De secans kan ontwikkeld worden in.
The longest side of the triangle is called the hypotenuse so the formal definition is. Die stelling is as volg. In mathematics the Pythagorean theorem or Pythagoras theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangleIt states that the area of the square whose side is the hypotenuse the side opposite the right angle is equal to the sum of the areas of the squares on the other two sidesThis theorem can be written as an equation relating the.
A² b² c². Al bij de oude Grieken ging meetkunde echter ook om getallen voorgesteld als verhouding tussen lijnstukken. De secans van een scherpe hoek in een rechthoekige driehoek is dus de reciproke van de cosinus van deze hoek.
Een perfect getal of volmaakt getal is een positief natuurlijk getal dat gelijk is aan de som van zijn echte delers niet het getal zelf. Carl Friedrich Gauss oorspronkelijk Gauß Brunswijk 30 april 1777 Göttingen 23 februari 1855 was een Duits wiskundige en natuurkundige die een zeer belangrijke bijdrage heeft geleverd aan een groot aantal deelgebieden van de wiskunde en de exacte wetenschappen waaronder de getaltheorie statistiek analyse differentiaalmeetkunde geodesie elektrostatica. Naast de standaard wetenschappelijke rekenmachine die u hier onder ziet kunt u gratis gebruik maken van de BTW Rekenmachine en de Stelling van Pythagoras Rekenmachine.
Chinese waarnemers noteerden de verschijning van een komeet uit het Oosten in 1059 vChr de oudst bekende vermelding. 500 vChr was een van de presocratische filosofenRond 540 vChr. Pythagoras bewees voor het eerste de stelling van Pythagoras en construeerde op algebraïsch wijze de pythagorese drietallen.
In China bestaat een oude traditie van sterrenkunde. De Oude Grieken kenden alleen de eerste vier perfecte. Ondersteunde formules en vergelijkingen.
Formule voor de omtrek van een driehoek. Oefenen met getallen tussen 2. Areaal omtrek sinus- en cosinusregel hypotenusa perimeter stelling van Pythagoras oppervlakte en volume.
Wat is het volume van een cilinder met een straal van 4 cm en een hoogte van 8 cm. Haal het beste uit jezelf. Uit de goniometrische cirkel en de stelling van Pythagoras kan de volgende relatie met de tangens afgeleid worden.
De stelling van Pythagoras is een van de bekendste wiskunde formules. Hoeken stelling van Pythagoras Kwadratische vergelijkingen Wortel. De Griekse wiskunde vormt een belangrijke periode in de geschiedenis van wiskunde fundamenteel door de geavanceerde meetkunde en het idee van het formeel bewijs.
Pythagorean theorem the well-known geometric theorem that the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse the side opposite the right angleor in familiar algebraic notation a2 b2 c2. De som van het kwadraat van de lengtes van de rechthoekszijden is gelijk aan het kwadraat van de lengte van de schuine zijde. Fermats equation x n y n z n with positive integer solutions is an example of a Diophantine equation named for the 3rd-century Alexandrian mathematician Diophantus who studied them and developed methods for the solution of some kinds of Diophantine equationsA typical Diophantine problem is to find two integers x and y such that their sum and the sum of their.
Daar is deze website op gebaseerd. Is de som van alle echte delers van dan is een perfect getal als. Emigreerde hij naar het Zuid-Italiaanse Croton waar hij politiek geëngageerd was en een religieus-filosofische broederschap oprichtte die enige invloed had op het maatschappelijk levenVanwege moeilijkheden met de stedelingen.
Machtreeks. And conversely if a point D on the side BC of triangle ABC divides BC. Vind de diameter van een bol met een volume van 1984 liter.
Bhāskara II staat vooral bekend voor zijn bewijs van de stelling van Pythagoras. Stelling van Pythagoras Met de stelling van Pythagoras kun je de lengtes van de zijden van een rechthoekige driehoek berekenen. Wheel with liquid demonstrates the Pythagorean theorem at Brentwood.
Probeer GRATIS online en test je kennis. Pythagoras was verantwoordelijk voor verschillende opmerkelijke stellingen en gaf leiding aan een geheimzinnige religieuze groep. Voor een juiste berekening moet de.
Pythagoras aangetoond met kwadraat zijden. A and b are the other two sides. Wij bieden u gemak overzicht en snelheid.
Pythagoras se Stelling is n wiskundige stelling wat vernoem is na die Griekse wiskundige PythagorasVolgens tradisie het Pythagoras die stelling ontdek en bewys maar die stelling se resultaat was voor Pythagoras se ontdekking aan verskeie antieke bevolkings bekend waaronder die Egiptenare en die Indiërs. Afstand in de gewone meetkunde Afstand tussen twee punten. Van een scherpe hoek in een rechthoekige driehoek is de secans gelijk aan.
In enige reghoekige driehoek. Pythagoras was een Griekse wiskundige die leefde in de 6 de eeuw voor Christus. De studie van de ruimte begint met de meetkunde in het bijzonder de Euclidische meetkunde.
1 is een echte deler. Is de som van alle positieve delers van dus inclusief 1 en zelf dan is perfect als. Consider a triangle ABCLet the angle bisector of angle A intersect side BC at a point D between B and CThe angle bisector theorem states that the ratio of the length of the line segment BD to the length of segment CD is equal to the ratio of the length of side AB to the length of side AC.
Wat kun je in een vreemde taal als je een bepaald taalniveau hebt. Het ERK werd in 2001 ontwikkeld door de Raad van Europa en heeft sindsdien een belangrijke plek gekregen in het Nederlandse talenonderwijs. De stelling van Pythagoras geldt voor rechthoekige driehoeken waarvan de rechthoekszijden willekeurige reële getallen zijn en de Oude Grieken wisten al dat de schuine zijde niet altijd commensurabel is met de rechthoekszijden zelfs als deze laatsten gehele getallen zijn.
In de gewone euclidische meetkunde is de kortste verbindingsweg of euclidische afstand een rechte lijn en kan de afstand worden berekend als de wortel uit de som van de kwadraten van de verschillen tussen de coördinaten volgens de stelling van Pythagoras. In een tweedimensionale ruimte. Zij hadden echter een bijzondere voorkeur voor meetkundige figuren waarvan de zijden wél.
De Stelling van Pythagoras berekenen kan iedereen. A 2 b 2 c 2. Pythagoras was een wiskundige wetenschapper astronoom en filosoof uit het oude Griekenland die leefde in de zesde eeuw voor Christus.

Reken En Wiskunde Filmpjes Over Pythagoras
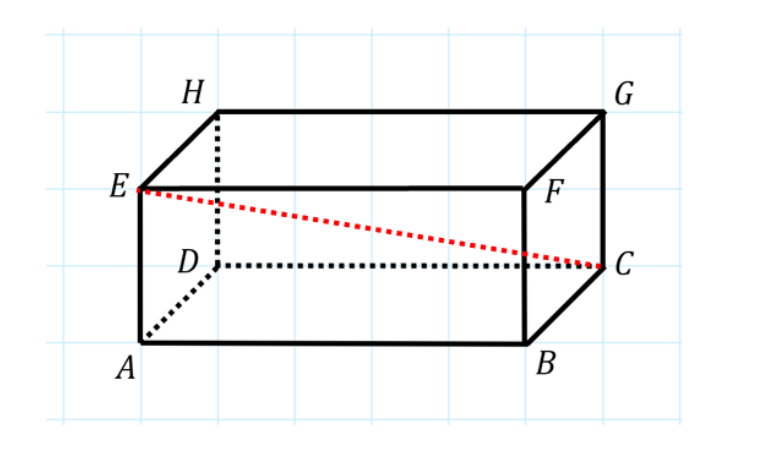
De Uitgebreide Stelling Van Pythagoras Wrts

Stelling Van Pythagoras Hoe Werkt Het Mr Chadd Academy
1 Inleiding Wiskunde Stelling Van Pythagoras

Stelling Van Pythagoras Wiskunde Uitleg
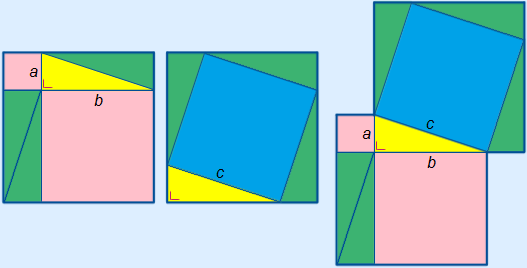
Stelling Van Pythagoras Theorie Wiskunde
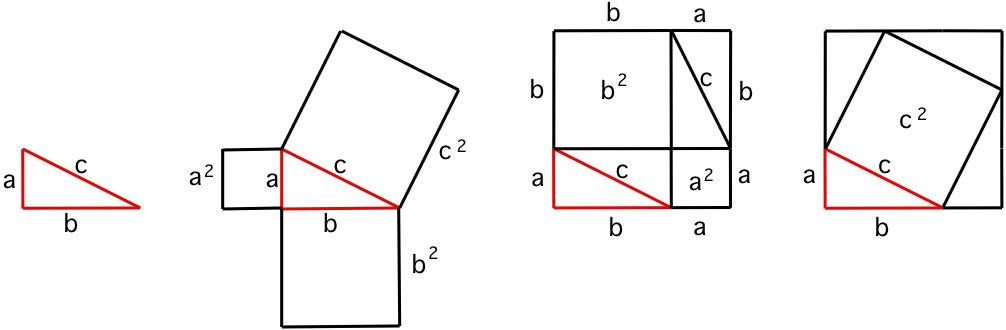
Bewijs Van De Stelling Van Pythagoras
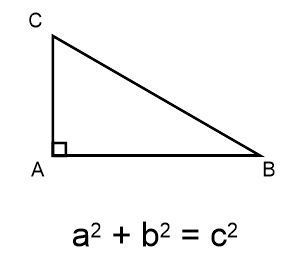
Uitleg Stelling Van Pythagoras Note
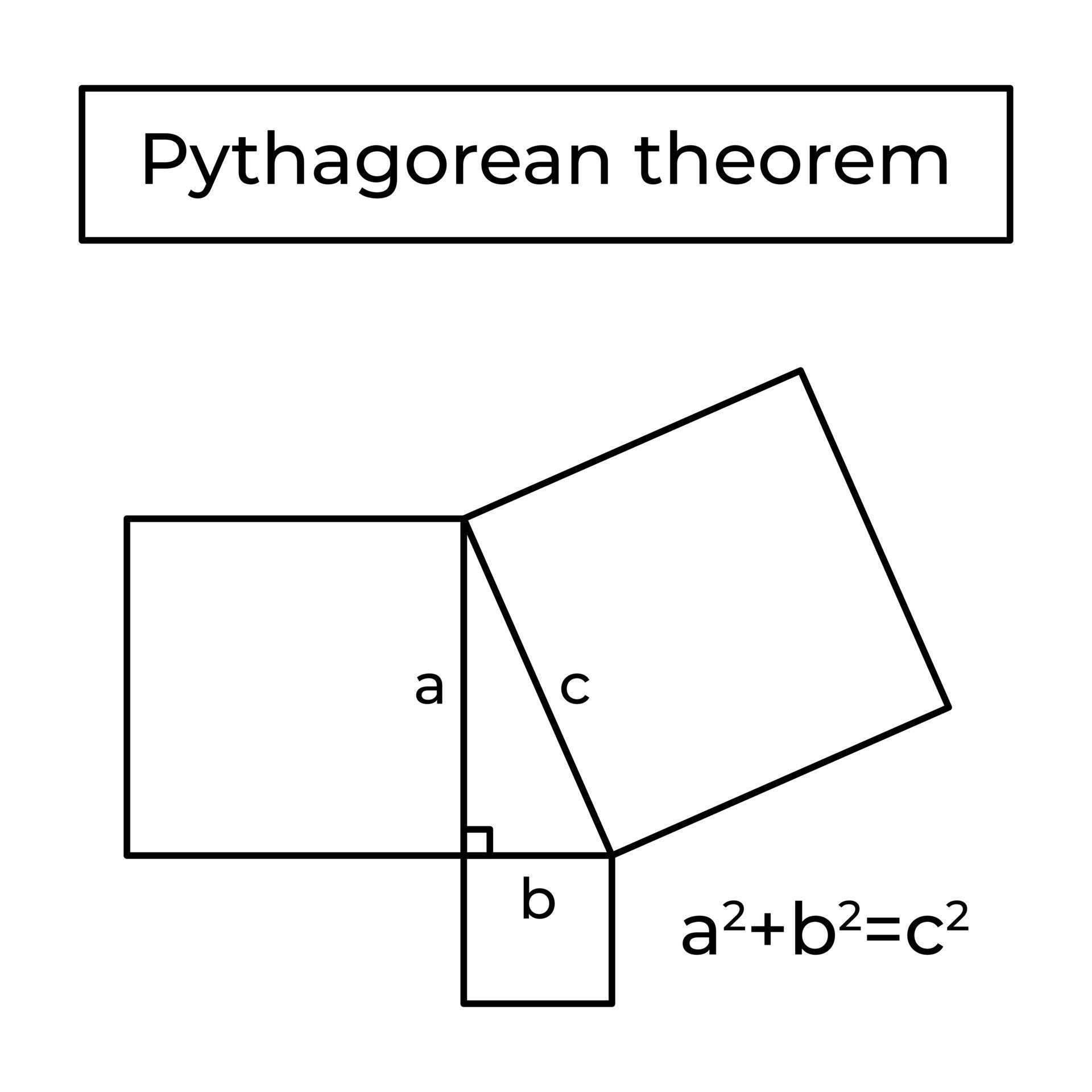
Stelling Van Pythagoras Euclides Bewijs En Formule Rechthoekige Driehoek Basisschool Geometrie Vectorillustratie Geisoleerd Op Een Witte Achtergrond 5851720 Download Free Vectors Vector Bestanden Ontwerpen Templates
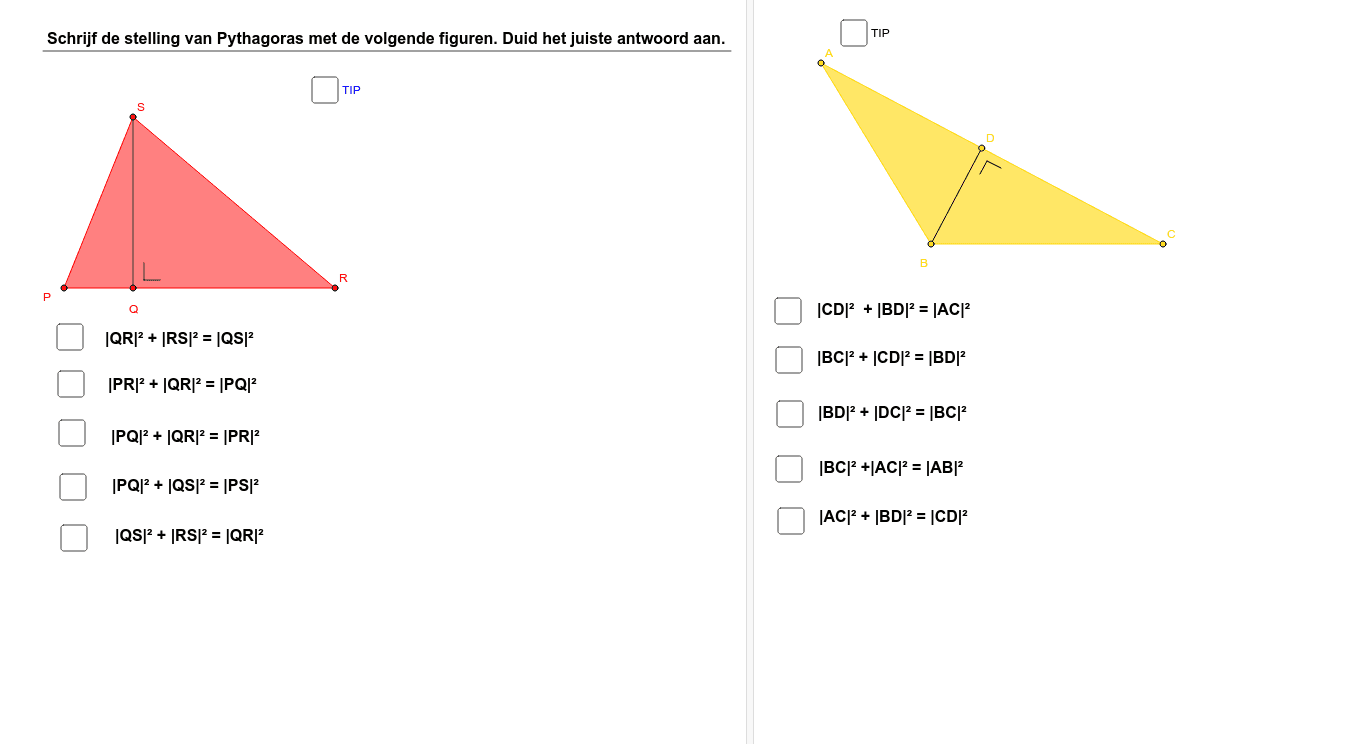
Stelling Van Pythagoras Oefening 1 Geogebra

Stelling Van Pythagoras Ppt Download Stelling Van Pythagoras Ppt Driehoeken
Een Ander Bewijs Voor De Stelling Van Pythagoras
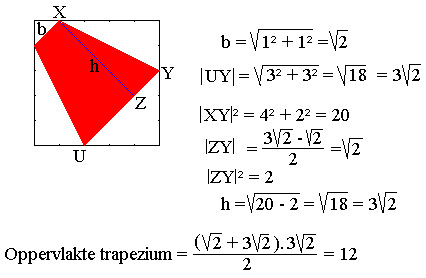
Vraag 15 Toepassing Stelling Van Pythagoras
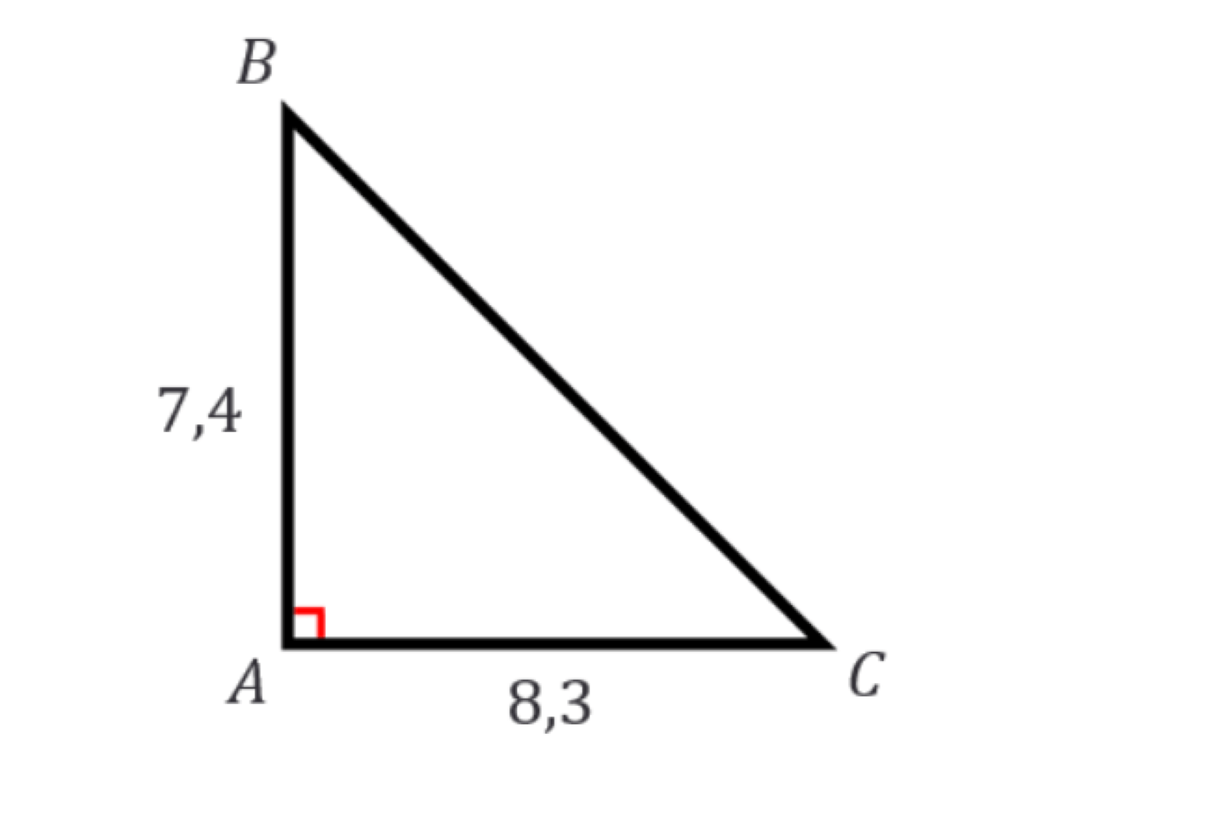
Samenvatting Van De Stelling Van Pythagoras Uit Getal En Ruimte 2 Havo Vwo 10 Wrts

De Stelling Van Pythagoras Ppt Download
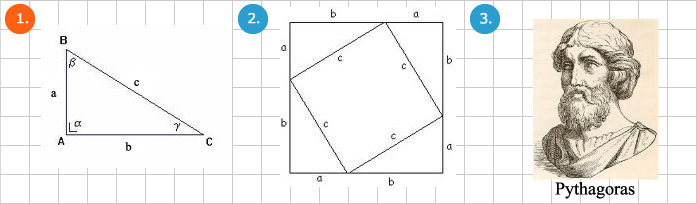
Stelling Van Pythagoras Wiskunde Net

5 4 Pythagoras Gebruiken Wiskundeuitleg Dhr Verhoeff Het Streek College